Expanding the Capabilities of Reinforcement Learning via Text Feedback

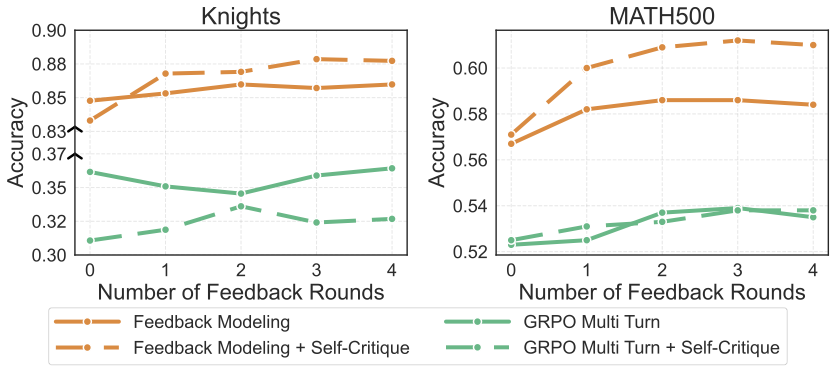
Overview of Reinforcement Learning from Text Feedback (RLTF). The framework uses a feedback provider (judge) to generate critiques $c_0$ on the policy's first-turn output $y_0$. RLTF-SD (Self Distillation) trains the policy to match the feedback-conditioned second-turn generations $y_1$, and RLTF-FM (Feedback Modeling) predicts the critiques $c_0$ as an auxiliary objective. Both methods improve single-turn test-time performance by internalizing feedback during training.

Abstract

The success of RL for LLM post-training stems from an unreasonably uninformative source: a single bit of information per rollout as binary reward or preference label. At the other extreme, distillation offers dense supervision but requires demonstrations, which are costly and difficult to scale. We study text feedback as an intermediate signal: richer than scalar rewards, yet cheaper than complete demonstrations. Textual feedback is a natural mode of human interaction and is already abundant in many real-world settings, where users, annotators, and automated judges routinely critique LLM outputs. Towards leveraging text feedback at scale, we formalize a multi-turn RL setup, RL from Text Feedback (RLTF), where text feedback is available during training but not at inference. Therefore, models must learn to internalize the feedback in order to improve their test-time single-turn performance. To do this, we propose two methods: Self Distillation (RLTF-SD), which trains the single-turn policy to match its own feedback-conditioned second-turn generations; and Feedback Modeling (RLTF-FM), which predicts the feedback as an auxiliary objective. We provide theoretical analysis on both methods, and empirically evaluate on reasoning puzzles, competition math, and creative writing tasks. Our results show that both methods consistently outperform strong baselines across benchmarks, highlighting the potential of RL with an additional source of rich supervision at scale.

Reinforcement Learning from Text Feedback (RLTF)

This problem is naturally formulated as a multi-turn setting: the model generates an attempt, feedback is appended to form an extended prompt, and the model revises. The natural objective to optimize is the multi-turn objective, which maximizes expected sum of rewards over an $H$-turn interaction:

\[ J_{\text{MultiTurn}}(\pi) = \mathbb{E}^{\pi}\left[\sum_{h=0}^{H-1} r_h\right] \]

However, at test time, feedback is often unavailable, in the sense that users want good outputs on the first try. Therefore, our goal is to improve single-turn competence, so we define the single-turn objective:

\[ J_{\text{SingleTurn}}(\pi) = \mathbb{E}_{x_0 \sim \mu}\left[\mathbb{E}_{y \sim \pi(\cdot|x_0)}[R(x_0, y)]\right] \]

The central research question is: Given access to feedback-augmented trajectories during training, how can we design learning objectives and algorithms that improve $J_{\text{SingleTurn}}(\pi)$?

Self Distillation (RLTF-SD)

Text feedback can turn an incorrect first attempt into a correct second attempt. We convert this feedback-conditioned generation into improvement on the single-turn metric via Self Distillation: we treat the policy acting under the second-turn prompt as a teacher, and distill it into the original policy.

For each initial prompt $x_0$, we sample a first-turn output $y_0 \sim \pi(\cdot | x_0)$, obtain feedback $c_0$, and form the feedback-augmented prompt $x_1 = f(x_0, y_0, c_0)$. We then sample a revised output $y_1 \sim \pi(\cdot | x_1)$ and use $y_1$ to update $\pi(\cdot | x_0)$ (not $\pi(\cdot | x_1)$).

Feedback Modeling (RLTF-FM)

We can treat the critique itself as a supervision signal and explicitly model the feedback provider. Feedback Modeling trains the policy to predict the feedback itself, providing dense token-level gradients on failure rollouts.

To do this, we define a feedback-prediction distribution $p_\pi(c | x, y) := \pi(c | f_{\text{FeeMol}}(x, y))$. Because the feedback model uses the same LM, it enables test-time scaling via self-feedback: the model can generate its own critiques and perform iterative refinement at inference time.

Self Distillation Loss

Distill feedback-conditioned
2nd turn into 1st turn

$$\nabla\ell_{\text{distill}}^{\text{awr}}(\pi)=\mathbb{E}_{y_1\sim\pi(\cdot\mid x_1)}\!\left[A(y_1)\,\nabla\log\pi(y_1\mid x_0)\right]$$

with first-turn baseline: $A^{(0)}(y_1):=R(x_0,y_1)-\frac{1}{N}\sum_{j=1}^{N}R(x_0,y_0^j)$

Converts second-turn generation → training signal

Feedback Modeling Loss

Predict the critique as
auxiliary objective

$$\ell_{\text{FeeMol}}(\pi) := \mathbb{E}^\pi\Bigg[\textstyle\sum_{h=0}^{H-1} -\log p_\pi(c_h | x_h, y_h)\Bigg]$$

Combined: $\max_\pi J_{\text{MultiTurn}}(\pi) - \lambda_{\text{FeeMol}} \ell_{\text{FeeMol}}(\pi)$

Enables test-time scaling via self-feedback

Key Results

We evaluate on three domains: reasoning puzzles (Knights and Knaves, Binary Matrix, Shortest Path), competition math (MATH500, AIME24), and creative writing (LitBench, WritingBench).

Performance comparison across reasoning, math, and creative writing benchmarks
Benchmark	Base Model	GRPO Single-turn	GRPO Multi-turn	Feedback Descent	RLTF-SD	RLTF-FM
Reasoning
Knights and Knaves	0.058	0.373	0.352	0.055	0.802	0.880
Binary Matrix	0.001	0.125	0.950	0.005	0.976	0.978
Shortest Path	0.034	0.385	0.384	0.035	0.830	0.905
Math
MATH500 (DAPO)	0.376	0.526	0.523	0.415	0.548	0.567
AIME24 (DAPO)	0.025	0.058	0.025	0.045	0.088	0.083
MATH500 (DeepMath)	0.376	0.558	0.578	0.424	0.598	0.636
AIME24 (DeepMath)	0.025	0.042	0.050	0.054	0.058	0.058
Creative Writing
LitBench	4.20	6.83	6.41	8.25	8.80	8.40
WritingBench	5.71	5.92	6.29	5.30	6.71	6.39

Main findings:

Both RLTF-SD and RLTF-FM consistently outperform all baselines across tasks, demonstrating the effectiveness of learning from text feedback.
Naive multi-turn GRPO shows similar single-turn performance to single-turn training, suggesting that naively incorporating feedback as additional context is insufficient to internalize its learning signal.
RLTF-SD excels in creative writing tasks where teacher-student distribution mismatch is small.
RLTF-FM performs better on math and reasoning tasks where the auxiliary prediction loss is easier to optimize.
Semantically rich text feedback is critical—replacing it with correctness-only feedback significantly degrades performance.

Ablation: Text Feedback vs. Correctness-Only Feedback

A key question is whether the semantic richness of text feedback matters, or whether simply knowing correctness is sufficient. We compare RLTF-SD using full text critiques against a correctness-only baseline that replaces the judge's critique with a simple sentence: "Your previous answer was {correct/incorrect}".

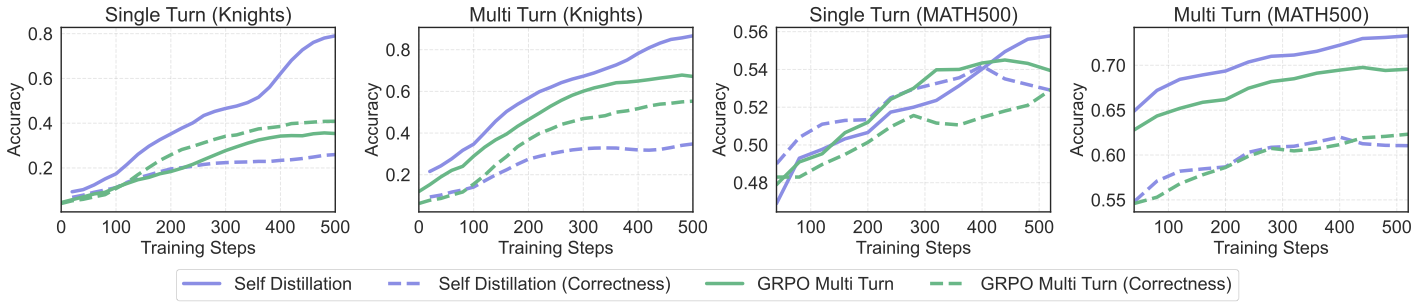
Reinforcement Learning from Text Feedback

Figure: Evaluation curves on Knights and Knaves and MATH500 (trained on DAPO) for text feedback vs. correctness-only feedback. We compare single- and multi-turn accuracy on two algorithms: multi-turn GRPO and RLTF-SD. Overall, using text feedback outperforms using correctness-only feedback for single-turn and multi-turn accuracy on both algorithms.

Key findings:

The correctness-only baseline does not perform well compared to RLTF-SD with full text feedback, indicating that semantically rich text feedback is critical.
One notable exception is the single-turn Knights and Knaves accuracy using multi-turn GRPO. Without distillation, neither text feedback nor correctness-only feedback can significantly influence the model's first-turn response, so there is little difference between the two in this setting.

Test-Time Scaling via Self-Feedback

A unique advantage of RLTF-FM (Feedback Modeling) is that it enables test-time scaling via self-feedback. Because the model learns to predict critiques during training, it can generate its own feedback at inference time and perform iterative refinement—without requiring an external judge.

We evaluate the model trained with RLTF-FM on Knights and Knaves and MATH500 by allowing it to generate up to 5 rounds of self-feedback at inference time. We compare against a baseline that uses RL to improve the model's self-critique using second-turn reward, with early termination disabled during training.

Figure: Test-time scaling results on Knights and Knaves and MATH500 (trained on DAPO). The x-axis shows the number of self-feedback rounds at inference time. We compare RLTF-FM with multi-turn scalar-based RL, where the dashed line ("+ Self-Critique") denotes further using RL to improve the self-critique during training.

Key findings:

Self-critique RL alone is insufficient: In the math experiment, GRPO with and without self-critique training achieve similar test-time improvement, suggesting that simply training the model to critique itself with RL does not provide meaningful gains.
RLTF-FM enables significant test-time improvement: Adding the feedback modeling loss in addition to self-critique RL training brings substantial test-time improvement, demonstrating that learning to predict critiques transfers to better self-improvement capabilities.
Improvement saturates after a few rounds: The benefit of RLTF-FM is mainly in terms of the magnitude of improvement, not in terms of the number of rounds. Test-time improvement saturates after a handful of rounds, which corroborates findings from the self-improvement literature.